Bài viết này cung cấp kiến thức toàn diện về Tam Giác Ngoại Tiếp, từ định nghĩa cơ bản đến các bài tập nâng cao, giúp học sinh nắm vững và tự tin giải quyết mọi dạng toán liên quan.
1. Định Nghĩa Tam Giác Ngoại Tiếp
Tam giác ngoại tiếp một đường tròn là tam giác có ba cạnh tiếp xúc với đường tròn đó. Ngược lại, đường tròn được gọi là đường tròn nội tiếp tam giác. Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác.
Hình ảnh minh họa trực quan về một tam giác ngoại tiếp đường tròn, thể hiện rõ các cạnh của tam giác tiếp xúc với đường tròn tại một điểm duy nhất.
Đường tròn nội tiếp tam giác là đường tròn lớn nhất nằm hoàn toàn bên trong tam giác.
2. Tính Chất Quan Trọng Của Tam Giác Ngoại Tiếp
Các tính chất sau đây vô cùng quan trọng khi giải bài toán về tam giác ngoại tiếp:
- Tiếp tuyến: Mỗi cạnh của tam giác là một tiếp tuyến của đường tròn nội tiếp.
- Đường phân giác: Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác.
- Khoảng cách: Khoảng cách từ tâm đường tròn nội tiếp đến mỗi cạnh của tam giác bằng bán kính của đường tròn.
- Diện tích: Diện tích tam giác ngoại tiếp có thể được tính bằng công thức: S = pr, trong đó p là nửa chu vi tam giác và r là bán kính đường tròn nội tiếp.
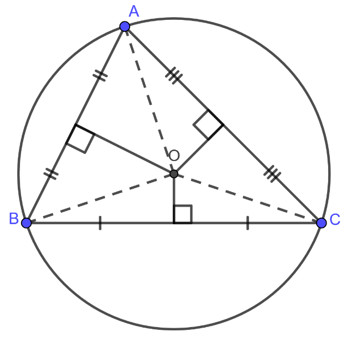
Hình ảnh minh họa tâm của đường tròn nội tiếp tam giác, đồng thời làm nổi bật tính chất tâm này là giao điểm của ba đường phân giác trong tam giác.
3. Các Khái Niệm Liên Quan Đến Tam Giác Ngoại Tiếp
Để hiểu sâu hơn về tam giác ngoại tiếp, cần nắm vững các khái niệm sau:
3.1. Bán Kính Đường Tròn Nội Tiếp
Bán kính đường tròn nội tiếp (r) có thể được tính bằng nhiều công thức, tùy thuộc vào thông tin đã biết:
- Công thức diện tích: r = S/p, trong đó S là diện tích tam giác và p là nửa chu vi.
- Công thức Heron: Nếu a, b, c là độ dài ba cạnh của tam giác, thì r = √( (p-a)(p-b)(p-c) / p ), với p = (a+b+c)/2.
3.2. Tính Chất Tiếp Tuyến
Tiếp tuyến từ một điểm đến đường tròn có độ dài bằng nhau. Điều này có nghĩa là nếu từ một đỉnh của tam giác kẻ hai tiếp tuyến đến đường tròn nội tiếp, thì độ dài của hai tiếp tuyến đó bằng nhau.
3.3. Ứng Dụng Trong Các Bài Toán
Tam giác ngoại tiếp thường xuất hiện trong các bài toán chứng minh, tính toán diện tích, bán kính, và các yếu tố hình học khác. Việc nắm vững các tính chất và công thức liên quan là chìa khóa để giải quyết các bài toán này một cách hiệu quả.
4. Bài Tập Về Tam Giác Ngoại Tiếp
Dưới đây là một số bài tập ví dụ về tam giác ngoại tiếp, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán:
Bài 1: Cho tam giác ABC có độ dài ba cạnh là AB = 5cm, BC = 7cm, CA = 8cm. Tính bán kính đường tròn nội tiếp tam giác ABC.
Bài 2: Chứng minh rằng trong một tam giác ngoại tiếp, các đường thẳng nối các đỉnh với tiếp điểm trên cạnh đối diện đồng quy tại một điểm (điểm Gergonne).
Bài 3: Cho tam giác ABC ngoại tiếp đường tròn (O; r). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn với các cạnh BC, CA, AB. Chứng minh rằng AD, BE, CF đồng quy.
Hình ảnh minh họa phương trình đường tròn liên quan đến tam giác ngoại tiếp, giúp hình dung mối liên hệ giữa các yếu tố hình học và đại số trong bài toán.
Bài 4: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính bán kính đường tròn nội tiếp tam giác ABC.
Bài 5: Cho tam giác ABC có diện tích S và nửa chu vi p. Chứng minh rằng bán kính đường tròn nội tiếp r = S/p.
5. Kết Luận
Hiểu rõ về tam giác ngoại tiếp và các tính chất liên quan là nền tảng quan trọng để giải quyết nhiều bài toán hình học. Hy vọng bài viết này cung cấp cho bạn kiến thức cần thiết và hữu ích trong quá trình học tập.