Phương trình 5/3x+2=2x-1 là một ví dụ điển hình của phương trình tuyến tính một ẩn. Bài viết này sẽ cung cấp một hướng dẫn chi tiết về cách giải phương trình này một cách dễ hiểu nhất. Chúng ta sẽ đi qua từng bước, từ việc đặt phương trình đến tìm ra nghiệm cuối cùng.
Để bắt đầu, hãy xem xét cấu trúc của phương trình 5/3x+2=2x-1. Mục tiêu của chúng ta là tìm giá trị của ‘x’ sao cho hai vế của phương trình bằng nhau.
Đầu tiên, chúng ta cần di chuyển tất cả các số hạng chứa ‘x’ về một vế và các hằng số về vế còn lại. Điều này giúp chúng ta đơn giản hóa phương trình.
Bước 1: Thu gọn phương trình
Chúng ta có thể trừ cả hai vế của phương trình cho 2x:
5/3x + 2 – 2x = 2x – 1 – 2x
Điều này cho chúng ta:
5/3x – 2x + 2 = -1
Tiếp theo, chúng ta chuyển số 2 sang vế phải bằng cách trừ cả hai vế cho 2:
5/3x – 2x = -1 – 2
Vậy ta có:
5/3x – 2x = -3
Bước 2: Quy đồng mẫu số
Để cộng hoặc trừ các số hạng chứa ‘x’, chúng ta cần quy đồng mẫu số. Trong trường hợp này, mẫu số chung là 3. Chúng ta viết lại 2x thành 6/3x:
5/3x – 6/3x = -3
Bước 3: Thực hiện phép tính
Bây giờ chúng ta có thể thực hiện phép trừ:
(5/3 – 6/3)x = -3
-1/3x = -3
Bước 4: Tìm giá trị của x
Để tìm giá trị của ‘x’, chúng ta nhân cả hai vế của phương trình cho -3:
(-1/3x) -3 = -3 -3
Điều này cho chúng ta:
x = 9
Kết luận:
Vậy nghiệm của phương trình 5/3x+2=2x-1 là x = 9. Bạn có thể kiểm tra lại bằng cách thay x = 9 vào phương trình ban đầu để đảm bảo rằng cả hai vế đều bằng nhau.
Giải phương trình đại số là một kỹ năng quan trọng trong toán học. Hy vọng rằng hướng dẫn này đã giúp bạn hiểu rõ hơn về cách giải phương trình 5/3x+2=2x-1.
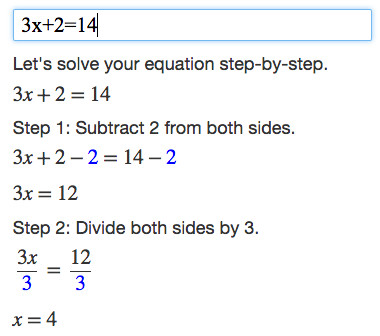
Để minh họa thêm cách giải các phương trình tương tự, bạn có thể tham khảo các công cụ giải toán trực tuyến. Ví dụ, bạn có thể nhập phương trình 3x+2=14 để xem các bước giải chi tiết.
Các công cụ này thường cung cấp lời giải từng bước, giúp bạn hiểu rõ hơn về quy trình giải toán.
Sau khi nhập phương trình, công cụ sẽ hiển thị các bước giải chi tiết, giúp bạn hiểu rõ cách tìm ra nghiệm.
Ngoài việc giải phương trình, các công cụ đại số còn có thể được sử dụng để vẽ đồ thị hàm số. Ví dụ, bạn có thể vẽ đồ thị của hai hàm số y=2x^2+1 và y=3x-1 trên cùng một hệ trục tọa độ để xem điểm giao nhau của chúng.
Các tính năng khác bao gồm đơn giản hóa đa thức. Ví dụ, bạn có thể nhập biểu thức x^2 + x + 2 + (2x^2 - 2x) để công cụ tự động thu gọn nó.
Cuối cùng, bạn có thể sử dụng công cụ để kiểm tra lại đáp án của mình. Ví dụ, nếu bạn giải phương trình 2x+3=7 và tìm ra x=2, bạn có thể nhập 2x+3=7 @ 2 để kiểm tra xem đáp án của bạn có đúng không.