Trong hình học và vật lý, phép cộng hai vecto là một phép toán cơ bản và quan trọng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về định nghĩa, tính chất và các ứng dụng của việc cộng hai vecto, giúp bạn nắm vững kiến thức và giải quyết các bài toán liên quan một cách hiệu quả.
1. Định Nghĩa Phép Cộng Hai Vecto
Để hiểu rõ về “2 Vecto Cộng Nhau”, trước tiên ta cần nắm vững định nghĩa. Phép cộng hai vecto tạo ra một vecto mới, gọi là vecto tổng.
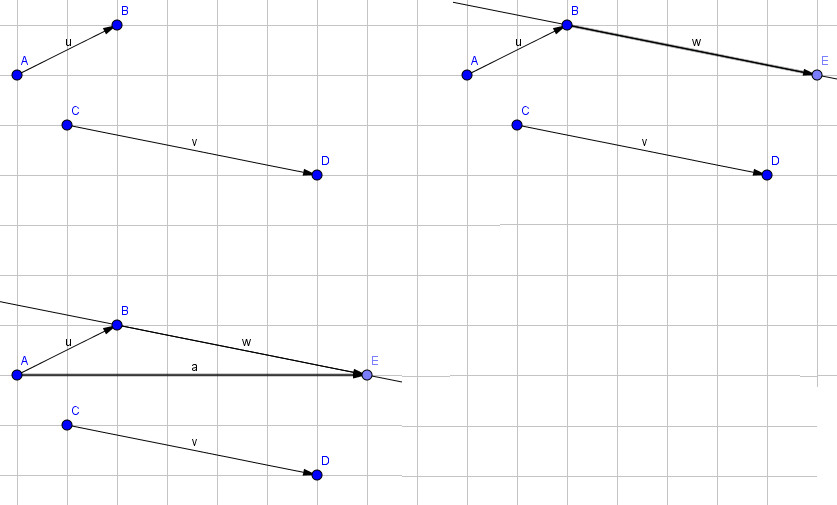
Định nghĩa: Cho hai vecto $vec{a}$ và $vec{b}$. Lấy một điểm A bất kỳ, vẽ $vec{AB} = vec{a}$ và $vec{BC} = vec{b}$. Khi đó, vecto $vec{AC}$ được gọi là tổng của hai vecto $vec{a}$ và $vec{b}$. Ký hiệu: $vec{AC} = vec{a} + vec{b}$.
Hình ảnh minh họa quy tắc cộng vecto, trong đó vecto tổng (AC) được tạo thành bằng cách nối đuôi hai vecto thành phần (AB và BC).
Ví dụ: Cho hình vuông ABCD, tính $vec{AB} + vec{BC}$.
Giải: $vec{AB} + vec{BC} = vec{AC}$.
2. Các Tính Chất Của Phép Cộng Vecto
Phép cộng vecto sở hữu các tính chất quan trọng, giúp đơn giản hóa các phép toán và chứng minh các đẳng thức liên quan.
- Tính giao hoán: $vec{a} + vec{b} = vec{b} + vec{a}$.
- Tính kết hợp: $(vec{a} + vec{b}) + vec{c} = vec{a} + (vec{b} + vec{c})$.
- Tính chất với vecto không: $vec{a} + vec{0} = vec{0} + vec{a} = vec{a}$.
3. Quy Tắc Hình Bình Hành
Quy tắc hình bình hành là một phương pháp đặc biệt để cộng hai vecto có chung điểm gốc.
Quy tắc: Nếu ABCD là hình bình hành, thì $vec{AB} + vec{AD} = vec{AC}$.
Hình ảnh minh họa quy tắc hình bình hành, trong đó vecto tổng (AC) là đường chéo của hình bình hành được tạo bởi hai vecto thành phần (AB và AD).
Ví dụ: Cho hình bình hành ABCD tâm I. Khẳng định nào sau đây đúng? $vec{AB} + vec{AD} = vec{AC}$.
4. Ứng Dụng Của Phép Cộng Hai Vecto
Phép cộng hai vecto có nhiều ứng dụng quan trọng trong hình học, vật lý và các lĩnh vực kỹ thuật.
4.1. Trong Hình Học
- Xác định trung điểm đoạn thẳng: I là trung điểm của đoạn thẳng AB khi và chỉ khi $vec{IA} + vec{IB} = vec{0}$.
- Xác định trọng tâm tam giác: G là trọng tâm của tam giác ABC khi và chỉ khi $vec{GA} + vec{GB} + vec{GC} = vec{0}$.
4.2. Trong Vật Lý
- Tổng hợp lực: Khi có nhiều lực tác động lên một vật, lực tổng hợp là tổng của các vecto lực đó.
- Tính vận tốc tương đối: Vận tốc của một vật so với một hệ quy chiếu khác được tính bằng phép cộng vecto vận tốc.
Hình ảnh minh họa sự tổng hợp của hai lực F1 và F2 thành lực tổng hợp F bằng quy tắc hình bình hành, thể hiện ứng dụng của phép cộng vecto trong vật lý.
5. Bài Tập Về Phép Cộng Hai Vecto
5.1. Dạng 1: Xác Định Vecto Tổng
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng $vec{AM} = frac{1}{2}(vec{AB} + vec{AC})$.
Giải:
$vec{AM} = vec{AB} + vec{BM} = vec{AB} + frac{1}{2}vec{BC} = vec{AB} + frac{1}{2}(vec{AC} – vec{AB}) = frac{1}{2}(vec{AB} + vec{AC})$.
5.2. Dạng 2: Chứng Minh Đẳng Thức Vecto
Ví dụ: Cho hình bình hành ABCD. Chứng minh rằng $vec{AB} + vec{AD} + vec{CB} + vec{CD} = vec{0}$.
Giải:
$vec{AB} + vec{AD} + vec{CB} + vec{CD} = (vec{AB} + vec{CD}) + (vec{AD} + vec{CB}) = (vec{AB} – vec{AB}) + (vec{AD} – vec{AD}) = vec{0}$.
Kết Luận
Hiểu rõ về “2 vecto cộng nhau” là nền tảng quan trọng để học tốt hình học vecto và ứng dụng vào các bài toán thực tế. Nắm vững định nghĩa, tính chất và các quy tắc cộng vecto sẽ giúp bạn tự tin giải quyết mọi bài tập liên quan. Hãy luyện tập thường xuyên để nâng cao kỹ năng và đạt kết quả tốt nhất trong học tập.