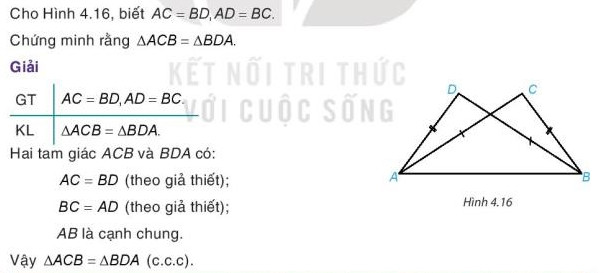
Hai tam giác bằng nhau là một khái niệm quan trọng trong hình học. Bài viết này sẽ trình bày chi tiết định nghĩa, các trường hợp bằng nhau thường gặp và các bài tập vận dụng giúp bạn hiểu rõ hơn về “2 Tam Giác Bằng Nhau”.
Hai tam giác, ví dụ ABC và A’B’C’, được gọi là bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau. Điều này có nghĩa là:
AB = A’B’, BC = B’C’, CA = C’A’
∠A = ∠A’, ∠B = ∠B’, ∠C = ∠C’
Khi đó, ta viết ΔABC = ΔA’B’C’.
Alt: Hình ảnh minh họa hai tam giác bằng nhau ABC và A’B’C’ với các cạnh và góc tương ứng được đánh dấu.
Các Trường Hợp Bằng Nhau Của Tam Giác
Để chứng minh hai tam giác bằng nhau, ta không nhất thiết phải chứng minh tất cả các cạnh và góc tương ứng bằng nhau. Thay vào đó, ta có thể sử dụng các trường hợp bằng nhau sau:
Trường Hợp Cạnh – Cạnh – Cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Alt: Mô tả trường hợp bằng nhau c.c.c, với ba cạnh của tam giác này bằng ba cạnh của tam giác kia.
Trường Hợp Cạnh – Góc – Cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Alt: Hình ảnh minh họa trường hợp bằng nhau c.g.c, hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia.
Trường Hợp Góc – Cạnh – Góc (g.c.g)
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Alt: Ví dụ về trường hợp bằng nhau g.c.g, một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Bài Tập Về Hai Tam Giác Bằng Nhau
Để củng cố kiến thức, chúng ta sẽ xem xét một số bài tập ví dụ:
Bài 1: Cho tam giác ABD và CBD có AB = BC, AD = CD, BD là cạnh chung. Chứng minh rằng ΔABD = ΔCBD.
Giải:
Xét hai tam giác ABD và CBD, ta có:
- AB = BC (giả thiết)
- AD = CD (giả thiết)
- BD là cạnh chung
Vậy ΔABD = ΔCBD (c.c.c)
Alt: Sơ đồ bài tập chứng minh hai tam giác ABD và CBD bằng nhau dựa trên trường hợp c.c.c.
Bài 2: Cho tam giác OAC vuông tại A và tam giác OBD vuông tại B, có OA = OB và góc AOC = góc BOD (đối đỉnh). Chứng minh rằng ΔOAC = ΔOBD.
Giải:
Xét hai tam giác vuông OAC và OBD, ta có:
- OA = OB (giả thiết)
- ∠AOC = ∠BOD (đối đỉnh)
Vậy ΔOAC = ΔOBD (g.c.g)
Alt: Hình vẽ bài tập chứng minh hai tam giác vuông OAC và OBD bằng nhau theo trường hợp góc cạnh góc.
Bài 3: Cho tam giác EFH và HGE có EF = HG, EG = HF, EH là cạnh chung. Chứng minh rằng ΔEFH = ΔHGE.
Giải:
Xét hai tam giác EFH và HGE, ta có:
- EF = HG (giả thiết)
- EG = HF (giả thiết)
- EH chung
Vậy ΔEFH = ΔHGE (c.c.c)
Alt: Sơ đồ bài toán chứng minh hai tam giác EFH và HGE bằng nhau dựa vào trường hợp cạnh cạnh cạnh.
Kết Luận
Hiểu rõ về “2 tam giác bằng nhau” và các trường hợp bằng nhau là nền tảng quan trọng để giải quyết các bài toán hình học phức tạp hơn. Việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp bạn nắm vững kiến thức và áp dụng linh hoạt vào thực tế.